非線形最小二乗法について詳しく解説

導入

非線形最小二乗法は、 m 個の観測値 ( m > n ) からnパラメーターの非線形モデルを推定することに特化した最小二乗法の形式です。このタイプの問題を推定する 1 つの方法は、初期モデルの線形化バージョンに基づいて連続する反復を考慮することです。

理論

m個の観測ペアのセットを考えます。

そして次のタイプの回帰関数 。この関数は説明的なxに依存しますが、 nパラメーターのベクトルにも依存します。 とパラメータベクトルを見つけたい最小二乗の意味で、データに最もよく適合するものは次のとおりです。

$$ {S=\sum_{i=1}^{m}r_i^2} $$

で最小化されます

ここで、残基r _{i は}次のように与えられます。

$$ {r_i= y_i – f(x_i, symbol \beta) } $$

のために

剰余Sの二乗和の最小値は、勾配が消滅したとき (必要な条件) に達します。問題はn 個のパラメータで定式化されるため、 n 個の正規方程式が存在します。

$$ {\frac{\partial S}{\partial \beta_j}=2\sum_i r_i\frac{\partial r_i}{\partial \beta_j}=0 \ (j=1,\ldots,n).} $$

非線形システムでは、導関数は

パラメータだけでなく説明変数にも依存します。したがって、線形の場合と同様に単純に正規方程式を解くことを諦めなければなりません。次に、反復プロセスを使用してデジタル解像度に頼ります。

$$ {symbol{\beta}^{k+1} = symbol{\beta}^k + \Delta symbol{\beta}.} $$

逐次近似を提供します

パラメータの真の（未知の）値にどんどん近づいていきます。 。

各反復で、初期モデルは次のテイラー展開によって線形化されます。

次のように：

$$ {f(x_i,symbol \beta_0) \approx f(x_i,symbol \beta^k) +\sum_j \frac{\partial f(x_i,symbol \beta^k)}{\partial \beta_{0,j}} \left(\beta_{0,j} -\beta^{k}_j \right) \approx f(x_i,symbol \beta^k) +\sum_j J_{ij} \Delta\beta_j. } $$

ヤコビ行列J はデータと現在の近似に依存するため、反復ごとに変化します。したがって、線形化モデルに関しては、

そして残差は次のように与えられます。

$$ {r_i=\Delta y_i- \sum_{j=1}^{n} J_{ij}\Delta\beta_j; \ \Delta y_i=y_i- f(x_i,symbol \beta^k).} $$

正規方程式は次のようになります。

$$ {-2\sum_{i=1}^{m}J_{ij} \left( \Delta y_i-\sum_{s=1}^{n} J_{is}\Delta \beta_s \right)=0} $$

あるいは

$$ {\sum_{i=1}^{m}\sum_{s=1}^{n} J_{ij}J_{is}\Delta \beta_s=\sum_{i=1}^{m} J_{ij}\Delta y_i \; (j=1,n).\,} $$

マトリックス的に言えば、次のようになります。

$$ {\mathbf{\left(J^TJ\right)\Delta symbol \beta=J^T\Delta y}.} $$

したがって、線形化により次のように書くことができます。

$$ {symbol{\beta}^{k+1} = symbol{\beta}^k + \left(\mathbf{J^TJ}\right)^{-1} \mathbf{J^T\Delta} y.} $$

右側の項全体は現在の反復のみに依存することに注意してください。

したがって、次の反復を見つけることができます。 。

残差の二乗の加重和を考慮することで、前のアプローチを簡単に一般化できます。

$$ {S=\sum_{i=1}^{m}W_{ii}r_i^2.} $$

理想的には、対角重み行列Wの各要素は観測分散の逆数に等しくなければなりません。その場合、正規方程式は次のようになります。

$$ {\mathbf{\left(J^TWJ\right)\Delta symbol \beta=J^TW\Delta y}} $$

これは、ガウス・ニュートン最適化アルゴリズムの基礎を提供します。

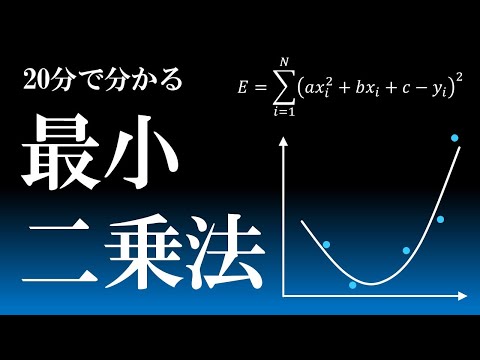
線形最小二乗法と非線形最小二乗法の違い

線形最小二乗法 (LCL) と非線形最小二乗法 (MCN) の間には多くの矛盾があります。

• MCN は反復プロセスであるため、開始点と停止基準が必要です。 MCL は直接 (線形代数) です。
• MCN では、ヤコビ行列 (一次導関数) を計算する必要があります。解析式を取得するのは複雑になる場合があります。この場合、数値微分が必要になります。
• 発散は MCN の一般的な問題です。実際、目的関数 (残差の二乗和) が反復ごとに増加することは珍しいことではありません。これは、テイラー展開による線形近似の精度が不足していることが原因である可能性があります。
• MCL の場合、解決策は固有ですが、MCN の場合は異なります。複数の (前提) 最小値が存在する可能性があります。

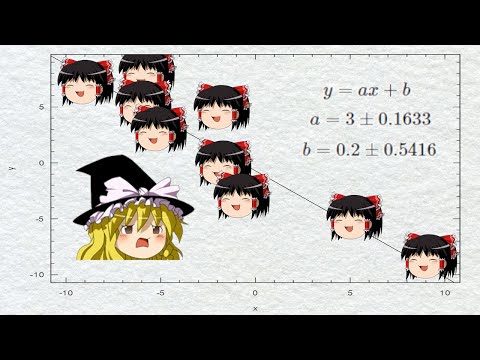
幾何学的解釈

線形最小二乗法の場合、目的関数Sはパラメータの二次関数です。

$$ {S=\sum_i W_{ii} \left(y_i-\sum_jX_{ij}\beta_j \right)^2} $$

β を推定するパラメータが 1 つである場合、関数Sは β 内の放物線になります。 2 つ以上のパラメータの場合、 Sの輪郭は同心円状の楕円で構成されます。ただし、行列

は正定値です。パラメータの最適値として到達した最小値は、これらの同心楕円の中心です。

非線形の場合、同心楕円の等高線は最小値付近でのみ当てはまります。これは、この場合、線形テイラー近似が目的関数の良好な近似であることが判明するためです。

$$ {S \approx\sum_i W_{ii} \left(y_i-\sum_j J_{ij}\beta_j \right)^2} $$

パラメーターが最適値から遠ざかるほど、輪郭は楕円体形状から大きく外れます。これは、初期近似を選択することが重要であることを意味します

最適値に近い反復プロセスの値ですが、定義上未知です。