導入


波動物理学、特に光学、音響学、地震学における屈折は、2 つの媒質間で速度が変化するときの波の偏向現象です。屈折は通常、2 つの媒体間の界面で、または媒体の密度またはインピーダンスの変化中に発生します。
このような波は2 つのアプローチで表現できます。
屈折の場合、2 つのモデルは同等ですが、最初のモデルは現象を説明し、2 番目のモデルは現象を定量化することを好みます。
説明
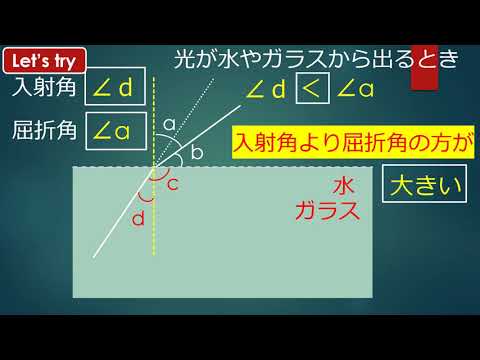
光は、ある透明な媒体から別の媒体に通過するときに偏向されます (たとえば、空気から水へ、またはその逆など)。これは、グラスに入れたストローを見るときに観察される現象です。ストローが壊れているように見えます。この明らかな亀裂が「屈折」という言葉の語源です。
光は「屈折」と呼ばれ、さまざまな透明な媒体を特徴付ける特性は「屈折率」であり、これは数値「屈折率」に変換されます。
波動アプローチ: ホイヘンス・フレネル原理
光の速度は 2 つの環境では同じではありません。この値の変化は、波の方向の変化を解釈するのに十分です。クリスチャン・ホイヘンスは、光の伝播と波面の伝播を関連付けたモデルを与え (1673 年)、バルトリンが観察したアイスランドの石材の複屈折を説明するためにそれを使用しました。
ホイヘンス・フレネルの原理
ホイヘンス・フレネルの原理は、界面では、第 1 媒質からの波が到達するすべての点が第 2 媒質で波を再放出すると述べています。したがって、屈折は、これらの再放射波のより低い (またはより速い) 速度に関連する波面の偏差として解釈できます。
ホイヘンスは、ニュートンに反対し、光は波であり、透明な媒体の中を段階的に伝播すると考えていました。彼は、波面をウェーブレットの重ね合わせとして想像しました。そのため、ジオプトリの通過時に、どちらの側でも速度が異なり、それに応じてウェーブレットのサイズが変更され、その結果、フロントが偏ることになります。環境指標の比率は、単純に有名度の比率として表示されます。
- $$ {\frac{n_1}{n_2} = \frac{v_2}{v_1}} $$
これと同じ原理を使用して、反射 (実際には、最初の媒質内で展開するウェーブレットの一部を考慮するだけで十分です) と回折を説明することもできます。
ホイヘンスの屈折光線の構築
この解釈により、幾何学的な構築も可能になります。これはデカルトのそれに似ていますが、セレブリティの比較に基づいています。
トレースされる光線は 1/n 1および 1/n 2であり、幾何学的推論は波面の共通交点 (点B ) に基づいており、本質的にウェーブレットに接している必要があります。
図中の最大のウェーブレットは、ジオプターがない場合 (ここでは n 2 > n 1 ) の波面の位置に対応し、したがって最小の円は回折波の前面に対応します。
したがって、屈折した光線は(IC)に従います ( I は入射点です)。
