導入
結晶構造(または結晶の構造) は、ブラレ格子、空間群、格子内の原子の位置のパラメータによって完全に記述されます。これらの原子は、空間群の対称操作の作用下で空間内で繰り返し、結晶構造を形成します。この構造は、科学技術の多くの分野の基本的な概念です。
結晶格子
結晶固体は、メッシュと呼ばれる原子または分子パターンの空間の 3次元での周期的な繰り返しで構成されています。壁紙が同じパターンの繰り返しで構成されているのと同じです。したがって、結晶構造の周期性は、規則的に配置された点のセットによって表されます。この集合を結晶格子と呼び、それを構成する点を格子ノードと呼びます。
ネットワークの周期性により、ノードのペア( O 、 M ) はベクトルを定義します。
- $$ {\overrightarrow{OM} = m_1 \vec a_1 + m_2 \vec a_2 + m_3 \vec a_3 } $$
m 1 、 m 2 、 m 3は相対的な整数である。
Bravezネットワーク
Bravez ネットワークは、単一ノードから始まる基底ベクトルに沿った変換によって得られるノードのネットワークです。 Bravez格子は3次元で14種類(2次元では5種類)に分類され、結晶構造の周期性を表します。これは、結晶の空間群の作用に従って空間内で繰り返される、非対称単位を占める原子の最小セットから得られます。すべての結晶材料は、これらの格子のいずれかに対応する周期性を持っています (準結晶は除く)。 14 種類の 3 次元ブラレ格子を次の表に示します。
| 網状系 | ネットワークの種類 | |||
| 三斜晶系または無閉晶系 |  プリミティブ ( aP ) | |||
| 単斜晶系 |  原始的 ( mP ) |  中心 (ミリ秒) | ||
| 斜方晶系 |  原始的 ( oP ) |  基底中心 ( oS ) |  中央揃え ( oI ) | 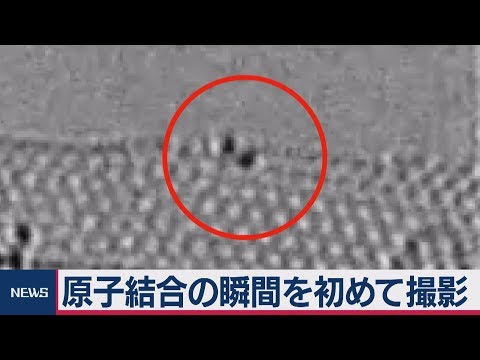 面中心 ( oF ) |
| 六角 | 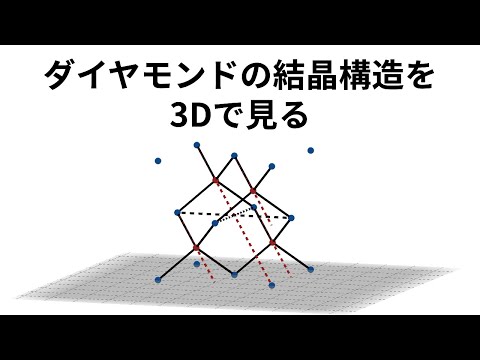 プリミティブ ( hP ) | |||
| 菱面体晶系 |  原生的 | |||
| 正方晶(または二次) | ||||
| 立方体(または等角) | ||||
要素メッシュ
基本メッシュ(またはプリミティブ) は、ネットワークの単一ノードを含む最小ボリュームのメッシュです。空間の 3 次元におけるこのメッシュの周期的な繰り返しは、ネットワーク全体と構造を再現するのに十分です。多くの場合、便宜上の理由から、または対称性をより強調するために、結晶を記述するために、複数のノードを含む、したがって基本的ではない複数のメッシュを使用します。
基本セルは、3 つの線形独立ベクトルa 、 b 、 cによって定義されます。これら 3 つのベクトルの選択は一意ではないため、ネットワークの対称性を多かれ少なかれ適切に示すことができるいくつかの基本セルを定義できます。
