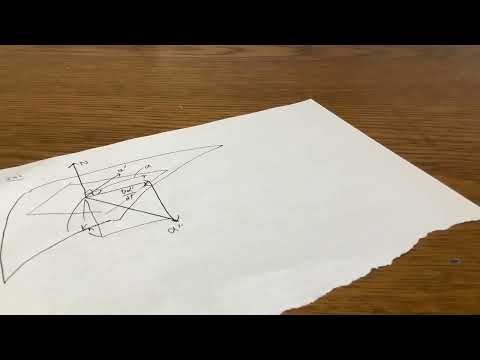
導入
幾何学では、測地線は、メトリック (距離を測定する手段) が指定された空間内の 2 点間の最短パス、または最短パスが複数ある場合はそのうちの 1 つを指定します。この距離の概念を変更すると、空間の測地線はまったく異なる外観を呈する可能性があります。

導入
もともと、測地線という用語は、地球の大きさと形状を測定する科学である測地学(ギリシャ語の「地球」という意味のgaiaと「分かち合う、分割する」というdaieinに由来) に由来しています。したがって、測地線は、測量士向けに、空間 (地理的な意味) の 2 点間の最短経路として指定されます。
数学への置き換えにより、測地線は「直線」の概念を「曲線空間」に一般化したものになります。したがって、測地線の定義は「曲面空間」のタイプに依存し、以前の受け入れは、この空間に計量がある場合にのみ局所的に当てはまります。
曲線空間内の 2 点間の最短経路は、曲線の長さの方程式を書き、その値の最小値を見つけることによって取得できます。同様に、別の値、つまり曲線のエネルギーを定義し、それを最小化しようとすることができ、その結果、測地線についても同じ方程式が得られます。直観的には、2 点間に張られた弾性バンドを想像することによって、この2 番目の定式化を理解することができます。弾性バンドが測地線に従っている場合、最小の長さ、つまり最小のエネルギーを持つことになります。
測地線は、リーマン幾何学、より一般的には計量幾何学の研究でよく出てきます。物理学では、測地線は自由粒子の動き、つまり、粒子が外部の力(一般相対性理論の枠組みにおける重力以外) を受けていないときの動きを記述します。特に、落石がたどる経路、周回衛星、または惑星軌道の形状はすべて、一般相対性理論の測地線によって記述されます。一方、ロケットで月に向かう宇宙飛行士の軌道は、機械のエンジンによって推力が発揮されるため、測地線ではありません。
幾何学的アプリケーション
メートル幾何学
計量幾何学では、測地線は局所的なあらゆる場所の最小距離に従う曲線です。より正確には、単位間隔Iから計量空間Mまでのパラメトリック曲線γ: I → M は、すべての条件が満たされるような定数v ≥ 0が存在する場合、測地線となります。
これは、リーマン多様体の測地線の概念を一般化します。ただし、計量幾何学では、考慮される測地線にはほとんどの場合、 v = 1および v = 1 という事実によって定義される自然パラメータ化が装備されています。

(擬似)リーマン幾何学
擬似リーマン多様体では、測地線M は、独自の接線ベクトルを平行に運ぶ規則的なパラメータ化曲線γ( t )によって定義されます。
これが何を意味するかを直観的に理解するには、地球の周りを一定の高度で飛行し、パリから北京まで最短ルートで向かう旅客機を想像してみてください。乗客の視点から見ると、飛行機の方向は常に同じです。旅行の終わりに、乗客は方向を変えるような加速度をまったく感じなかった。彼らによれば、彼らは最短ルートを選択したという。しかし、地球を中心とした基準系を考えると、飛行機の速度を表すベクトルは、惑星の形状に従うように時間の経過とともに方向を変えています。航空機が移動する幾何学形状に適応した方法での航空機の速度ベクトルのこの変更は、平行輸送が意味するものに正確に対応します。
数学用語では、これは次のように表されます。γ (λ) は測地線を表すパラメーター化された曲線であり、
座標x μに対応する基準系内の曲線への接線ベクトル (旅行者の基準系で時間とともにλ を特定する場合の速度ベクトル)
ここで、 ∇ はM上の Levi-Civita 接続です (共変導関数に相当します)。
この定義とレヴィ-チヴィタ接続の成分式から、測地方程式が得られます。
したがって、測地線は、さまざまな形で、この微分方程式に応答するパラメトリック曲線になります。 Γ α γβ はクリストッフェル記号であり、計量テンソルg に直接依存します。これらは、平坦な空間と比較して空間の微小な変形を表します。
最初の定式化を直感的に理解するには、オペレーターが
測地方程式は、曲線のエネルギーに関連付けられたオイラー ラグランジュ方程式でもあります。
ラグランジアンL (λ,γ, V ) = g γ ( V , V ) は時間 λ に依存しないため、ハミルトニアンは測地線に沿って保存されます。しかし、ここでハミルトニアンはラグランジアンに等しく、それ自体は速度ノルムの二乗に等しい。加速度が存在しないことと一致して、速度は測地線に沿って保存されると結論付けます。